
The unit vector in the direction of is denoted by. Unit VectorĪ vector whose modulus is unity, is called a unit vector. Vectors other than the null vector are called proper vectors. If and are two vectors, then the subtraction of from is defined as the vector sum of and - and is denoted by -Ī vector whose initial and terminal points are coincident is called zero or null or a void vector. This is known as the triangle law of addition of vectors which states that, if two vectors are represented in magnitude and direction by the two sides of a triangle taken in the same order, then their sum is represented by the third side taken in the reverse order. If and are two vectors, then the addition of from is denoted by + Vectors are generally denoted by (read as vector a, vector b, vector c,…)Ī quantity having only magnitude is called a scalar. The point A is called initial point of the vector and B is called the terminal point. Vectors are represented by directed line segments such that the length of the line segment is the magnitude of the vector and the direction of arrow marked at one end denotes the direction of the vector.Ī vector denoted by = is determined by two points A, B such that the magnitude of the vector is the length of the line segment AB and its direction is that from A to B.
#Null vector example plus
Therefore, we’ve shown for any vector 𝐮 and zero vector of equal dimension, 𝐳 plus 𝐮 will be equal to 𝐮 and 𝐮 plus 𝐳 will also be equal to 𝐮.A quantity having both magnitude and direction is called a vector.Įxample: velocity, acceleration, momentum, force, weight etc. And we know that adding zero doesn’t change a value, so this just gives us the vector 𝐮 one, 𝐮 two, all the way up to 𝐮 𝑛, which was our vector 𝐮. We just add the corresponding components of these two vectors together.īut all of the components of 𝐳 are zero, so we just get the vector zero plus 𝐮 one, zero plus 𝐮 two, all the way up to zero plus 𝐮 𝑛.
#Null vector example how to
So for example, if 𝐳 was the 𝑛-dimensional zero vector - so that’s just a vector of 𝑛 components, all of which are equal to zero - and 𝐮 is also a vector of 𝑛 dimensions - we’ll call the components 𝐮 one and 𝐮 two all the way up to 𝐮 𝑛 - then we know how to add these two vectors together. We could have proven this directly from component addition of two vectors. We would still get the vector 𝐮.Īnd there is one more way we could have proven this.

We know that vector addition is commutative, so we could actually add these in the opposite order.

Therefore, we’ve shown the zero vector plus the vector 𝐮 will just be equal to the vector 𝐮.Īnd we can also point out something else here. Since graphically, the zero vector doesn’t represent movement at all, moving along the zero vector and then moving along the vector 𝐮 will always just be equal to the vector 𝐮. So it doesn’t really matter how we draw our vector 𝐮. So our zero vector doesn’t represent movement in any direction. But we know all components in the zero vector are equal to zero. First, we’ll want to draw our zero vector. We can use this to find an expression for the zero vector plus the vector 𝐮. And although in this case our sketch is in two dimensions, this is also true in any number of dimensions. Then the vector 𝐯 plus 𝐮 will be the vector starting at the initial point of vector 𝐯 and ending at the terminal point of vector 𝐮. First, we sketch the vector 𝐯 and then at the terminal point of vector 𝐯, we sketch the vector 𝐮. Recall, we can add two vectors 𝐯 and 𝐮 graphically. However, it’s actually easier to do this graphically. And it might be tempting to try and do this by adding the components together. We need to find an expression for the zero vector plus the vector 𝐮 for any vector 𝐮. So for example, the vector zero, zero will be the zero vector in two dimensions.
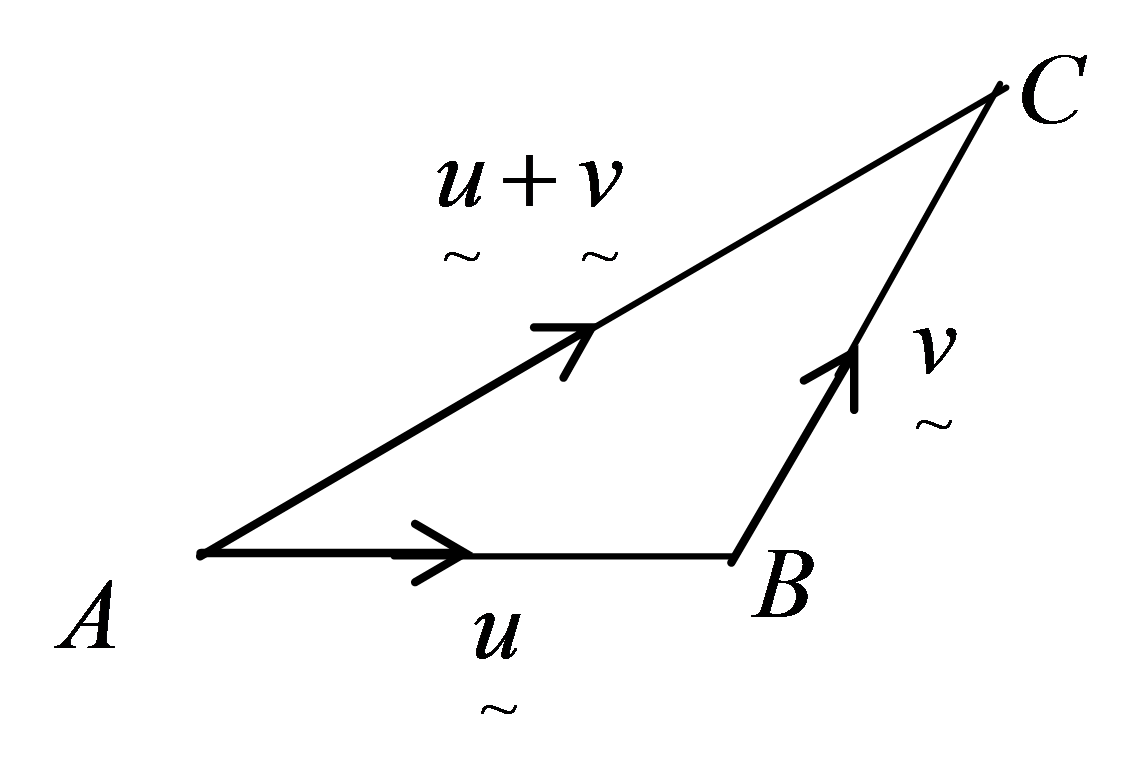
The zero vector is the vector which has all of its components equal to zero. Let’s start by recalling exactly what we mean by the zero vector. And there’s a few different ways we can do this. And we need to find an expression for the vector 𝐳 plus the vector 𝐮 for any vector 𝐮.

In this question, we’re told that 𝐳 is the zero vector. What is the vector 𝐳 plus the vector 𝐮 equal to for any vector 𝐮?


 0 kommentar(er)
0 kommentar(er)
